This thesis addresses optimal control of discrete-time switched linear
systems with application to networked embedded control systems (NECSs).
Part I focuses on optimal control and scheduling of discrete-time
switched linear systems. The objective is to simultaneously design a
control law and a switching (scheduling) law such that a cost function
is minimized. This optimization problem exhibits exponential complexity.
Taming the complexity is a major challenge. Two novel methods are
presented to approach this optimization problem: Receding-horizon
control and scheduling relies on the receding horizon principle. The
optimization problem is solved based on relaxed dynamic programming,
allowing to reduce complexity by relaxing optimality within predefined
bounds. The solution can be expressed as a piecewise linear (PWL) state
feedback control law. Stability is addressed via an a priori stability
condition based on a terminal weighting matrix and several a posteriori
stability criteria based on constructing piecewise quadratic Lyapunov
functions and on utilizing the cost function as a candidate Lyapunov
function. Moreover, a region-reachability criterion is derived. Periodic
control and scheduling relies on periodic control theory. Both offline
and online scheduling are studied. The optimization problem is solved
based on periodic control and exhaustive search. The online scheduling
solution can again be expressed as a PWL state feedback control law.
Stability is guaranteed inherently. Several methods are proposed to
reduce the online complexity based on relaxation and heuristics. Part II
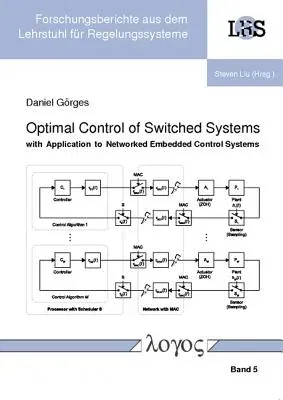
focuses on optimal control and scheduling of NECSs. The NECS is modeled
as a block-diagonal discrete-time switched linear system. Various
control and scheduling codesign strategies are derived based on the
methods from Part I regarding the structural properties of NECSs. The
methods presented in Part I and II are finally evaluated in a case
study.